Neat Factorization

I mentioned in class tonight a crazy method for factoring trinomials that I learned in grade school. I looked here for a reminder of it, since it was such a long time ago.

Here it is, in summary:

For starters, we have a generic trinomial.

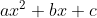
Instead of focusing on this equation, we are going to modify it to achieve this form:

Factor this equation, which is made easier by the lack of a large leading coefficient. It will factor into something that looks like this:

Now, plug in ax for each x in that factorization. Then, divide it by a. This is the necessary factorization for the original problem. In other words:

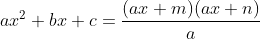
There are some requirements and proofs required to make sure that the a divides evenly from those two factors. But, even if it didn't, it's a successful factorization.