Starting and Ending with Applications

What can be done to interest a student in a topic in math? I think you show them how the things they do can be related to it. What can be done to make a student interested to continue to do math? You show them how to do something they've always wanted to do by using it. For example, let's take trigonometry and very simple vector applications (which a student would see in any physics class anyway). Trigonometry is a subject that people tend to hate, so I'll choose that one.

A lot of students these days play video games and computer games. One of the classic archetypes of such pastimes is the game from the first-person perspective. In a virtual world, such as the ones created by these games, in order to move right, you press the 'right arrow' button or key. In order to move forward, you press the 'up arrow'. However, some people have gained an edge over other players and seem to be able to move faster due to a trick. See, if they press both at the same time, they can travel diagonally significantly faster than they'd be able to otherwise. Woe to the person trying to flee from such a canny adversary in this game! This works because of vector addition and the rules of right triangles. If you want a game to remove this possible abuse, then how can you change it? The introduction is to use simple equal vectors (meaning the player travels at a 45-degree angle with respect to the direction their avatar faces). Students exposed to trigonometry need a solid background in right triangle geometry, and they can apply that here. It scales up into trig by saying that it doesn't make a whole lot of sense to be able to sidestep as quickly as you can run ahead, and in order to keep the total speed constant, you need to have some function that behaves periodically to monitor it.

The closing topic for trigonometry is to allow the students to try to do something they've wanted to do since you stepped into their lives--pelt you with water balloons. The ballistics of physics can be reduced to a few simple equations and students get a lot of practice solving for specific variables in computing ballistic trajectories. You can approach the problem by having students describe the qualitative behaviors they'd expect from throwing a ball at certain angles to hit a target. Then, you can show them the basic tools they need (they should not be expected to derive ballistic equations unless they've had significant exposure to calculus) in order to use what they've learned to try to hit you with some fun projectile. Some serious set-up is required to do this, since a means of reliably launching a projectile with specific force is sometimes difficult to come by. The trigonometry is in this in that they have to establish a specific angle required for the strength of the launcher, and achieving a simple expression for this requires the use of trig identities.

Physics teachers may complain that you're using up some of their tricks, but motivating a student to do something is a difficult task at times. It's possible, though, if you're willing to get your feet wet...

-Mark

Neat Factorization

I mentioned in class tonight a crazy method for factoring trinomials that I learned in grade school. I looked here for a reminder of it, since it was such a long time ago.

Here it is, in summary:

For starters, we have a generic trinomial.

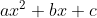Instead of focusing on this equation, we are going to modify it to achieve this form:

Factor this equation, which is made easier by the lack of a large leading coefficient. It will factor into something that looks like this:

Now, plug in ax for each x in that factorization. Then, divide it by a. This is the necessary factorization for the original problem. In other words:

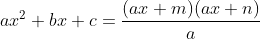There are some requirements and proofs required to make sure that the a divides evenly from those two factors. But, even if it didn't, it's a successful factorization.

"Why?"

One of the most fearsome elements in a student's arsenal is the question, "Why?" The power of this interrogation to discover is formidable. Its power to irritate is also great. It is, however, a question that every student should ask themselves whenever something seems wrong. It is not a bad thing for a student to ask, "Why am I learning this?" It's a great opportunity to tell them that it's not pointless. They open up to the possibility of its being used, and the teacher supplies the use.

It is therefore advantageous for a teacher of mathematics to know the utility of each item in a curriculum. It also behooves such a teacher to understand the value of the lessons in mathematics as a whole. While I cannot cover all of the applications of each segment of school math, I can try to address some of the benefits of the classes as a whole.

Mathematics can teach you how to think. This does not mean that everyone will learn to think by doing math, and it certainly doesn't mean that in order to learn to think, you must do math. It is merely one of many subject areas where prolonged exposure develops logic, reason, and memory. Students who would think well using the math model might discover that they have difficulty thinking with other models. It would be a disservice to these students to not permit them the mathematical mind.

Aside from fundamental cognition, mathematics teaches a student to fluidly apply tools to a variety of situations. A fairly elementary problem in ballistics would be nightmarish and impossible without a functional grasp of the concepts of arithmetic, algebra, and (sometimes) calculus. One of the profound mysteries behind mathematics is that it relates to our world at all. Teaching a student to tie the mathematical tools to the real-world concepts that they can sense and recognize is invaluable and I can scarcely believe that anyone gets by without this skill.

Consider a simple problem of paying in change for something. You can count how much you have. The number you get is clearly representative of the value of the money you have. You can physically move the appropriate amount of money for the transaction, counting it out, and then you can again physically count the money you have to get the new number that represents the value. This last step is, of course, simplified dramatically if a student can draw the connection between doling out change and the arithmetic process of subtraction. However, that is not something that should be expected to come naturally to a student. If you really dig down into that, there's no proof that it should be related at all except for experiential coincidence. That's the kind of innovation mathematics can teach you, and you only get more tools as you continue advancing in it.

In fact, once someone is fully armed with school mathematics (arithmetic, geometry, algebra, trigonometry, and a little calculus), one can accomplish staggering feats of computation. The difficult part is actually translating the applicable data from the world into the recognizable forms with which these tools are used. You can take a demand curve from economics and with calculus you can easily discover what price you should charge to get you the maximum amount of money. No one's going to do any better than that! The difficulty is in obtaining that function where you want to apply the tool.

I've always said that mathematics is all about being as lazy as possible while giving up no ground. You cover all your tracks, but take as few steps as possible to get from one place to another. The fact is, school mathematics trivializes a great deal of work that would be required if one could not apply its tools to situations in the real world. This leaves more time for the fun stuff. We all want more time for the fun stuff.